

An orthocenter is a point where all the altitudes of the triangle intersect and it is denoted as H. An incenter is the point that is equidistant from the sides of the triangle and it is denoted as I. What is the Difference Between Centroid, Orthocenter, Circumcenter, and Incenter?Ī circumcenter is a point that is equidistant from all the vertices of the triangle and it is denoted as O. Whereas an orthocenter is a point where three altitudes of the triangle intersect. That point is also considered as the origin of the circle that is inscribed inside that circle. What is the Difference Between Orthocenter and Incenter?Īn incenter is a point where three angle bisectors from three vertices of the triangle meet. The circumcenter of a triangle is the point of intersection of the perpendicular bisector of the three sides. The orthocenter of a triangle is the point of intersection of all the three altitudes drawn from the vertices of a triangle to the opposite sides. No, the orthocenter and circumcenter of a triangle are different. Are Orthocenter and Circumcenter the Same? It is an important central point of a triangle and thus helps in studying different properties of a triangle with respect to sides, vertices, other important points like circumcenter, centroid, etc. Thus, clubbing the two words together here means center for the altitudes (right angles) of the triangle. The term "ortho" means "right" and the center means the midpoint. M(slope) = \( \frac \) Why is it Called an Orthocenter? Step 1: Calculate the slope of the sides of the triangle using the formula: H ( x, y) is the intersection point of the three altitudes of the triangle. PA, QB, RC are the perpendicular lines drawn from the three vertices P, Q, and R respectively of the △PQR. Let us consider a triangle PQR, as shown in the figure below.
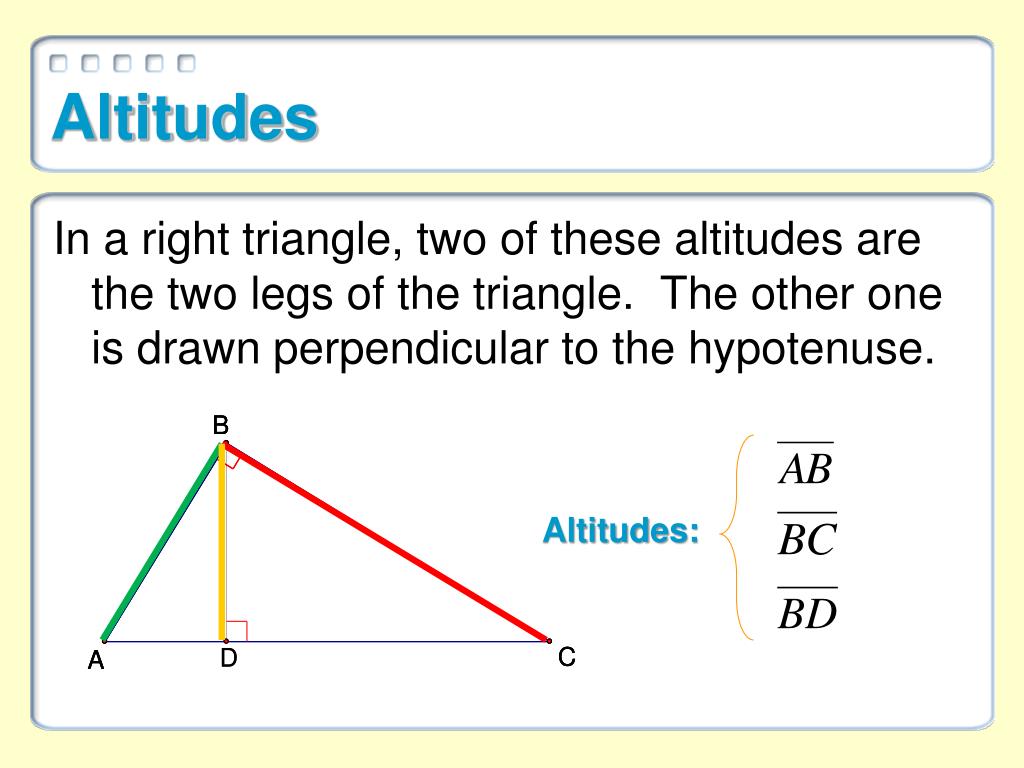
In the case of isosceles and equilateral triangles, a median bisects any angle at a vertex whose two. Every triangle has exactly three medians: one running from each vertex to the opposite side. The orthocenter formula helps in locating the coordinates of the orthocenter of a triangle. In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposing side. The product of the lengths of all these parts is equivalent for all three perpendiculars. Property 4: An orthocenter divides an altitude into different parts. As seen in the image below, the point of intersection lies at point C. Property 3: The orthocenter lies on the vertex of the right angle of the right triangle. As seen in the image below, the orthocenter formed by 3 intersecting lines or altitudes lies outside the triangle. Property 2: The orthocenter lies outside the triangle for an obtuse angle triangle. As seen in the below figure, the orthocenter is the intersection point of the lines PF, QS, and RJ. Property 1: The orthocenter lies inside the triangle for an acute angle triangle. For instance, for an equilateral triangle, the orthocenter is the centroid.
For some triangles, the orthocenter need not lie inside the triangle but can be placed outside. Dans ces domaines, l’accès aux données à référence spatiale ainsi qu’une connaissance des sources d’information et de leur qualité sont donc primordiales pour la conduite de projets.The properties of an orthocenter vary depending on the type of triangle such as the Isosceles triangle, Scalene triangle, right-angle triangle, etc. Face au déploiement massif des cartes numériques et des nombreux services basés sur la localisation, il s’agit de rester critique et surtout de développer les capacités nécessaires afin de choisir les outils et jeux de géodonnées adaptés aux besoins professionnels.Ĭ’est dans cette optique que ce cours propose de développer les éléments fondamentaux de la géomatique en décrivant les domaines clés que sont: les références géodésiques, les techniques d’acquisition des géodonnées, la topométrie, la localisation par satellites et la modélisation et représentation du terrain.Ĭet enseignement est proposé aux futurs ingénieurs et architectes qui ont recours aux géodonnées pour la réalisation de projets d’aménagement, de construction, de gestion de l’environnement, de transport et de développement territorial. Le domaine de l’information géographique a également suivi ce mouvement en modernisant l’ensemble des supports, des plans, des cartes topographiques et de tous les types de données à référence spatiale. Les nouvelles technologies de l’information ont facilité l’accès à de nombreuses bases de données offrant au grand public, mais surtout aux professionnels, une multitude de services.


 0 kommentar(er)
0 kommentar(er)
